Многие к одному
Рисунок B-1. Обязательность на одном конце с необязательностью на другом
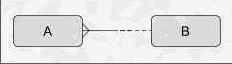
Это наиболее часто встречающаяся форма связи. Она предполагает, что каждое и любое вхождение сущности A может существовать только в контексте одного (и только одного) вхождения сущности B. С другой стороны, вхождения B могут существовать как в связи с вхождениями A, так и без оной.
Рисунок B-2. Необязательность на обоих концах
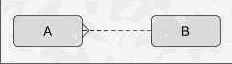
Применяется редко. Как A, так и B могут существовать без связи между ними.
Рисунок B-3. Обязательность на обоих концах
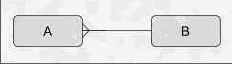
Достаточно сильная конструкция, предполагающая, что вхождение сущности B не может быть создано без одновременного создания по меньшей мере одного связанного с ним вхождения сущности A. В нашем примере БИЛЕТ становится таковым только тогда, когда он содержит по меньшей мере один КУПОН; до тех пор это только клочок бумаги.
Рисунок B-4. Необязательность на одном конце с обязательностью на другом
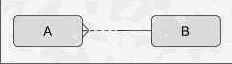
Редко используемая конструкция. Вероятнее всего имеет место, когда B представляет собой некоторое придуманное понятие, всегда включающее в себя точный набор вхождений A. При этом вхождения A могут уже существовать сами по себе. (При ближайшем рассмотрении эти связи зачастую оказываются связями типа "многие ко многим" - используйте для их проверки обратный синтаксис.)
